Basic concept

Censoring:right censoring

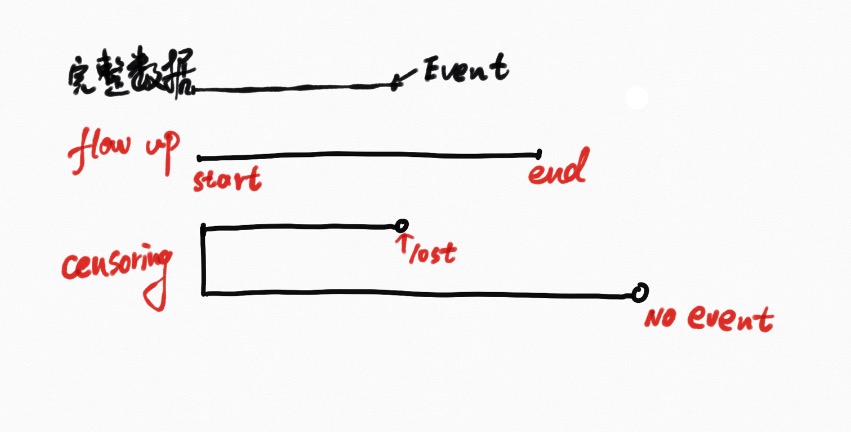
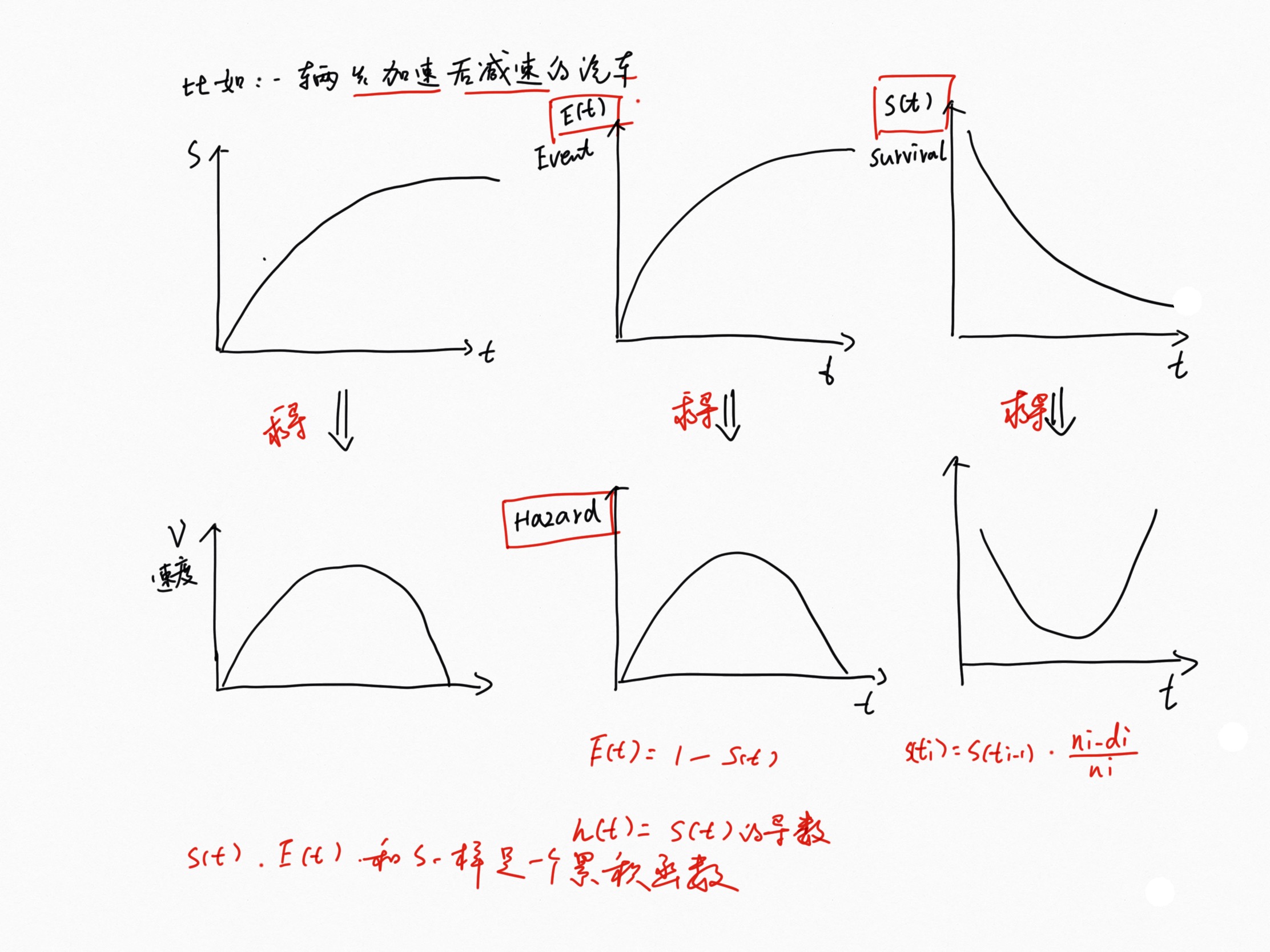
Survival and hazard functions

Survival analysis in R

#data
library("survival")
library("survminer")
data("lung")
#survival fit
fit <- survfit(Surv(time, status) ~ sex, data = lung)
#summary
summary(fit)$table

##       records n.max n.start events   *rmean *se(rmean) median 0.95LCL
## sex=1     138   138     138    112 325.0663   22.59845    270     212
## sex=2      90    90      90     53 458.2757   33.78530    426     348
##       0.95UCL
## sex=1     310
## sex=2     550

d <- data.frame(time = fit$time,
                  n.risk = fit$n.risk,
                  n.event = fit$n.event,
                  n.censor = fit$n.censor,
                  surv = fit$surv,
                  upper = fit$upper,
                  lower = fit$lower
                  )
head(d)

##   time n.risk n.event n.censor      surv     upper     lower
## 1   11    138       3        0 0.9782609 1.0000000 0.9542301
## 2   12    135       1        0 0.9710145 0.9994124 0.9434235
## 3   13    134       2        0 0.9565217 0.9911586 0.9230952
## 4   15    132       1        0 0.9492754 0.9866017 0.9133612
## 5   26    131       1        0 0.9420290 0.9818365 0.9038355
## 6   30    130       1        0 0.9347826 0.9768989 0.8944820

#Visualize survival curves
ggsurvplot(
   fit,                     # survfit object with calculated statistics.
   pval = TRUE,             # show p-value of log-rank test.
   conf.int = TRUE,         # show confidence intervals for 
                            # point estimaes of survival curves.
   conf.int.style = "step",  # customize style of confidence intervals
   xlab = "Time in days",   # customize X axis label.
   break.time.by = 200,     # break X axis in time intervals by 200.
   ggtheme = theme_light(), # customize plot and risk table with a theme.
   risk.table = "abs_pct",  # absolute number and percentage at risk.
  risk.table.y.text.col = T,# colour risk table text annotations.
  risk.table.y.text = FALSE,# show bars instead of names in text annotations
                            # in legend of risk table.
  ncensor.plot = TRUE,      # plot the number of censored subjects at time t
  surv.median.line = "hv",  # add the median survival pointer.
  legend.labs = 
    c("Male", "Female"),    # change legend labels.
  palette = 
    c("#E7B800", "#2E9FDF") # custom color palettes.
)

#Visualize cumulative events curves
ggsurvplot(fit,
          conf.int = TRUE,
          risk.table.col = "strata", # Change risk table color by groups
          ggtheme = theme_bw(), # Change ggplot2 theme
          palette = c("#E7B800", "#2E9FDF"),
          fun = "cumhaz")

#Log-rank test
surv_diff <- survdiff(Surv(time, status) ~ sex, data = lung)
surv_diff

## Call:
## survdiff(formula = Surv(time, status) ~ sex, data = lung)
## 
##         N Observed Expected (O-E)^2/E (O-E)^2/V
## sex=1 138      112     91.6      4.55      10.3
## sex=2  90       53     73.4      5.68      10.3
## 
##  Chisq= 10.3  on 1 degrees of freedom, p= 0.001

Concept

1. Kaplan-Meier curves and log-rank tests - are examples of univariate analysis.
2. Additionally, Kaplan-Meier curves and logrank tests are useful only when the predictor variable is categorical (e.g.: treatment A vs treatment B; males vs females). They don’t work easily for quantitative predictors such as gene expression, weight, or age.
3. Cox proportional hazards regression analysis, which works for both quantitative predictor variables and for categorical variables.

Compute the Cox model in R

#data

#fit
res.cox <- coxph(Surv(time, status) ~ sex, data = lung)
#summary
summary(res.cox)

## Call:
## coxph(formula = Surv(time, status) ~ sex, data = lung)
## 
##   n= 228, number of events= 165 
## 
##        coef exp(coef) se(coef)      z Pr(>|z|)   
## sex -0.5310    0.5880   0.1672 -3.176  0.00149 **
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
##     exp(coef) exp(-coef) lower .95 upper .95
## sex     0.588      1.701    0.4237     0.816
## 
## Concordance= 0.579  (se = 0.022 )
## Rsquare= 0.046   (max possible= 0.999 )
## Likelihood ratio test= 10.63  on 1 df,   p=0.001
## Wald test            = 10.09  on 1 df,   p=0.001
## Score (logrank) test = 10.33  on 1 df,   p=0.001

covariates <- c("age", "sex",  "ph.karno", "ph.ecog", "wt.loss")
univ_formulas <- sapply(covariates,
                        function(x) as.formula(paste('Surv(time, status)~', x)))
univ_models <- lapply( univ_formulas, function(x){coxph(x, data = lung)})
# Extract data 
univ_results <- lapply(univ_models,
                       function(x){ 
                          x <- summary(x)
                          p.value<-signif(x$wald["pvalue"], digits=2)
                          wald.test<-signif(x$wald["test"], digits=2)
                          beta<-signif(x$coef[1], digits=2);#coeficient beta
                          HR <-signif(x$coef[2], digits=2);#exp(beta)
                          HR.confint.lower <- signif(x$conf.int[,"lower .95"], 2)
                          HR.confint.upper <- signif(x$conf.int[,"upper .95"],2)
                          HR <- paste0(HR, " (", 
                                       HR.confint.lower, "-", HR.confint.upper, ")")
                          res<-c(beta, HR, wald.test, p.value)
                          names(res)<-c("beta", "HR (95% CI for HR)", "wald.test", 
                                        "p.value")
                          return(res)
                          #return(exp(cbind(coef(x),confint(x))))
                         })
res <- t(as.data.frame(univ_results, check.names = FALSE))
as.data.frame(res)

##            beta HR (95% CI for HR) wald.test p.value
## age       0.019            1 (1-1)       4.1   0.042
## sex       -0.53   0.59 (0.42-0.82)        10  0.0015
## ph.karno -0.016      0.98 (0.97-1)       7.9   0.005
## ph.ecog    0.48        1.6 (1.3-2)        18 2.7e-05
## wt.loss  0.0013         1 (0.99-1)      0.05    0.83

Multivariate Cox regression analysis

#fit
res.cox <- coxph(Surv(time, status) ~ age + sex + ph.ecog, data =  lung)
summary(res.cox)

## Call:
## coxph(formula = Surv(time, status) ~ age + sex + ph.ecog, data = lung)
## 
##   n= 227, number of events= 164 
##    (1 observation deleted due to missingness)
## 
##              coef exp(coef)  se(coef)      z Pr(>|z|)    
## age      0.011067  1.011128  0.009267  1.194 0.232416    
## sex     -0.552612  0.575445  0.167739 -3.294 0.000986 ***
## ph.ecog  0.463728  1.589991  0.113577  4.083 4.45e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
##         exp(coef) exp(-coef) lower .95 upper .95
## age        1.0111     0.9890    0.9929    1.0297
## sex        0.5754     1.7378    0.4142    0.7994
## ph.ecog    1.5900     0.6289    1.2727    1.9864
## 
## Concordance= 0.637  (se = 0.026 )
## Rsquare= 0.126   (max possible= 0.999 )
## Likelihood ratio test= 30.5  on 3 df,   p=1e-06
## Wald test            = 29.93  on 3 df,   p=1e-06
## Score (logrank) test = 30.5  on 3 df,   p=1e-06

sex_df <- with(lung,
               data.frame(sex = c(1, 2), 
                          age = rep(mean(age, na.rm = TRUE), 2),
                          ph.ecog = c(1, 1)
                          )
               )
sex_df

##   sex      age ph.ecog
## 1   1 62.44737       1
## 2   2 62.44737       1

# Survival curves
fit <- survfit(res.cox, newdata = sex_df)
ggsurvplot(fit, data=lung, conf.int = TRUE, legend.labs=c("Sex=1", "Sex=2"),
           ggtheme = theme_minimal())

1. the Schoenfeld residuals are independent of time, non-significant relationship between residuals and time

#From the output down, the test is not statistically significant for each of the covariates
res.cox <- coxph(Surv(time, status) ~ age + sex + wt.loss, data =  lung)
res.cox

## Call:
## coxph(formula = Surv(time, status) ~ age + sex + wt.loss, data = lung)
## 
##             coef exp(coef) se(coef)     z      p
## age      0.02009   1.02029  0.00966  2.08 0.0377
## sex     -0.52103   0.59391  0.17435 -2.99 0.0028
## wt.loss  0.00076   1.00076  0.00619  0.12 0.9024
## 
## Likelihood ratio test=14.67  on 3 df, p=0.002
## n= 214, number of events= 152 
##    (14 observations deleted due to missingness)

test.ph <- cox.zph(res.cox)
test.ph

##             rho chisq     p
## age     -0.0483 0.378 0.538
## sex      0.1265 2.349 0.125
## wt.loss  0.0126 0.024 0.877
## GLOBAL       NA 2.846 0.416

ggcoxzph(test.ph)

2. influential observations

hat(y) - y 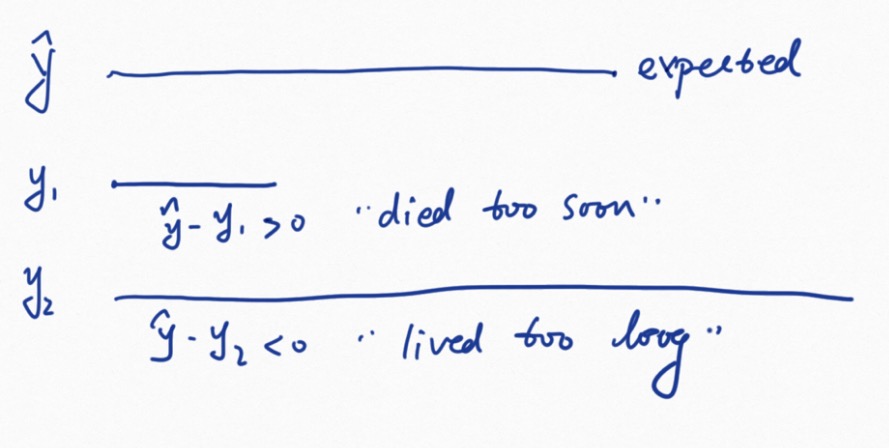1. Positive values correspond to individuals that “died too soon” compared to expected survival times. 2. Negative values correspond to individual that “lived too long”. 3. Very large or small values are outliers, which are poorly predicted by the model.

#type: the type of residuals to present on Y axis. Allowed values include one of c(“martingale”, “deviance”, “score”, “schoenfeld”, “dfbeta”, “dfbetas”, “scaledsch”, “partial”)
ggcoxdiagnostics(res.cox, type = "dfbeta",
                 linear.predictions = FALSE, ggtheme = theme_bw())

ggcoxdiagnostics(res.cox, type = "deviance",
                 linear.predictions = FALSE, ggtheme = theme_bw())

3.non linearity

we assume that continuous covariates have a linear form. However, this assumption should be checked Martingale residuals may present any value in the range (-INF, +1) : 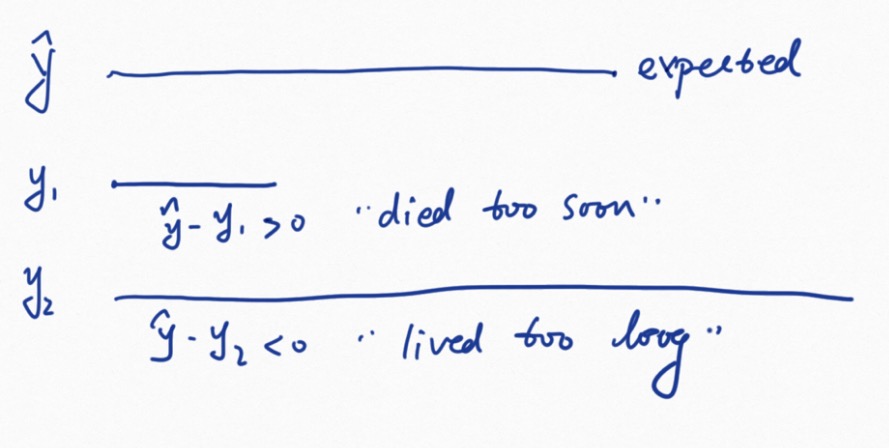1. A value of martinguale residuals near 1 represents individuals that “died too soon”, 2. and large negative values correspond to individuals that “lived too long”.

The function ggcoxfunctional() displays graphs of continuous covariates against martingale residuals of null cox proportional hazards model. This might help to properly choose the functional form of continuous variable in the Cox model . Fitted lines with lowess function should be linear to satisfy the Cox proportional hazards model assumptions.

#It appears that, nonlinearity is slightly here.
ggcoxfunctional(Surv(time, status) ~ age + log(age) + sqrt(age), data = lung)

#比较 变量age 在 线性age 和非线性 log(age) or sqrt(age) 下 残差分布模式图，基本一致，所以线性假设满足

reference

• survival analysis
• cox
• assumptions